【RL】Value-Based Learning

基于价值学习

Discounted Return

\[ \begin{aligned} U_t& =R_t+\gamma\cdot R_{t+1}+\gamma^2\cdot R_{t+2}+\gamma^3\cdot R_{t+3}+\gamma^4\cdot R_{t+4} \\ & =R_t+\gamma\cdot (R_{t+1}+\gamma^2\cdot R_{t+2}+\gamma^3\cdot R_{t+3}+\gamma^4\cdot R_{t+4}) \\ & =R_t+\gamma\cdot U_{t+1} \end{aligned} \]

Identity: $U_t=R_t+\gamma\cdot U_{t+1}$

TD Target

Assume $R_t$ depends on $(S_t, A_t, S_{t+1})$ \[ \begin{aligned} Q_\pi\left(s_t, a_t\right) & =\mathbb{E}\left[U_t \mid s_t, a_t\right] \\ & =\mathbb{E}\left[R_t+\gamma \cdot U_{t+1} \mid s_t, a_t\right] \\ & =\mathbb{E}\left[R_t \mid s_t, a_t\right]+\gamma \mathbb{\mathbb { E } [ U _ { t + 1 } | s _ { t } , a _ { t } ]} \\ & =\mathbb{E}\left[R_t \mid s_t, a_t\right]+\gamma \cdot \mathbb{E}\left[Q_\pi\left(s_{t+1}, A_{t+1}\right) \mid s_t, a_t\right] . \end{aligned} \] Identity: $Q_\pi(s_t,a_t)=\mathbb{E}[R_t+\gamma\cdot Q_\pi(S_{t+1},A_{t+1})]$ , for all $\pi$

左边是该动作的action-value function，右边含有期望，直接计算比较困难，故利用蒙特卡洛近似计算。

$R_t$ 近似为观测值$r_t$, $Q_\pi(S_{t+1},A_{t+1})$中$S_{t+1},A_{t+1}$都是随机变量，利用观测值$s_{t+1},a_{t+1}$近似 \[ R_t+\gamma\cdot Q_\pi(S_{t+1},A_{t+1}) \approx r_t+\gamma\cdot Q_\pi(s_{t+1},a_{t+1}) = TD\ target \] 期望$\mathbb{E}[R_t+\gamma\cdot Q_\pi(S_{t+1},A_{t+1})] \approx y_t$

TD learning: Encourage $Q_\pi(s_t,a_t)$ to approach $y_t$

因为$Q_\pi(s_t,a_t)$完全是估计，而$y_t$部分基于真实的奖励，相对于更加可靠

TD Error

\[ \delta_t=Q_\pi(s_t,a_t)-y_t \]

Sarsa

学习目标：更新$Q_\pi$ 使其更加接近真实值

每一轮迭代更新都依据五元组$(s_t,a_t,r_t,s_{t+1},a_{t+1})$更新$Q_\pi$

因此命名State-Action-Reward-State-Action（SARSA）

更新q-table时采用下一步真实的s‘和a’更新q值，也称为on-policy在线学习

表格形式

State和Action的数量是有限的（离散），通过一个表格来更新$Q_\pi$

每次更新表格中的一个元素，使得TD Error变小

Observe a transition $\left(s_t, a_t, r_t, s_{t+1}\right)$.
Sample $a_{t+1} \sim \pi\left(\cdot \mid s_{t+1}\right)$, where $\pi$ is the policy function.
TD target: $y_t=r_t+\gamma \cdot Q_\pi\left(s_{t+1}, a_{t+1}\right)$. 下一个动作的q值
TD error: $\delta_t=Q_\pi\left(s_t, a_t\right)-y_t$.
Update: $Q_\pi\left(s_t, a_t\right) \leftarrow Q_\pi\left(s_t, a_t\right)-\alpha \cdot \delta_t$.

算法：

代码实现

class SarsaTable():
    ....
    def learn(self, s, a, s_, a_):
        self.check_state_exist(s_)
        q = self.q_table.loc[s,a]
        if s_ != 'terminal':
            # 下个行动所采取的真实值
            q_ = r + self.gamma * self.q_table.loc[s_, a_]
            
            # Q learning 中采用下个阶段可能行动的最大值
            # q_ = r + self.gamma * self.q_table.loc[s_, :].max()
        else:
            q_ = r
        self.q_table.loc[s, a] += self.lr * (q_ - q)
        

def update():
    for epis in range(100):
        observation = env.reset()
        action = RL.choose_action(str(observation))
        while True:
            env.render()
            observation_, reward, done = env.step(action)

            # 获取下个阶段的action，并利用s_和a_同时更新参数
            action_ = RL.choose_action(str(observation_))
            RL.learn(str(observation), action, reward, str(observation_), action_)

            # 记录下个阶段的a_和s_
            observation = observation_
            action = action_

            if done:
                break

神经网络形式

价值网络$q(s,a;w)$是对动作价值函数$Q_\pi$的近似，利用sarsa算法更新网络参数

在actor-critic方法中用于对价值网络的参数进行改进

TD target: $y_t=r_t+\gamma \cdot q\left(s_{t+1}, a_{t+1} ; \mathbf{w}\right)$.

TD error: $\delta_t=q\left(s_t, a_t ; \mathbf{w}\right)-y_t$.

Loss: $\delta_t^2 / 2$.

Gradient: $\frac{\partial \delta_t^2 / 2}{\partial \mathbf{w}}=\delta_t \cdot \frac{\partial q\left(s_t, a_t ; \mathbf{w}\right)}{\partial \mathbf{w}}$.

Gradient descent: $\quad \mathbf{w} \leftarrow \mathbf{w}-\alpha \delta_t \cdot \frac{\partial q\left(s_t, a_t ; \mathbf{w}\right)}{\partial \mathbf{w}}$

Sarsa($\lambda$)

这种方法针对于表格形式Sarsa

Sarsa($\lambda$)就是更新获取到 reward 的前 lambda 步. lambda 是在 [0, 1] 之间取值。

不仅更新当前的$Q_\pi(s_t,a_t)$同时更新当前回合前面路径state-action的$Q_\pi(s,a)$

算法：

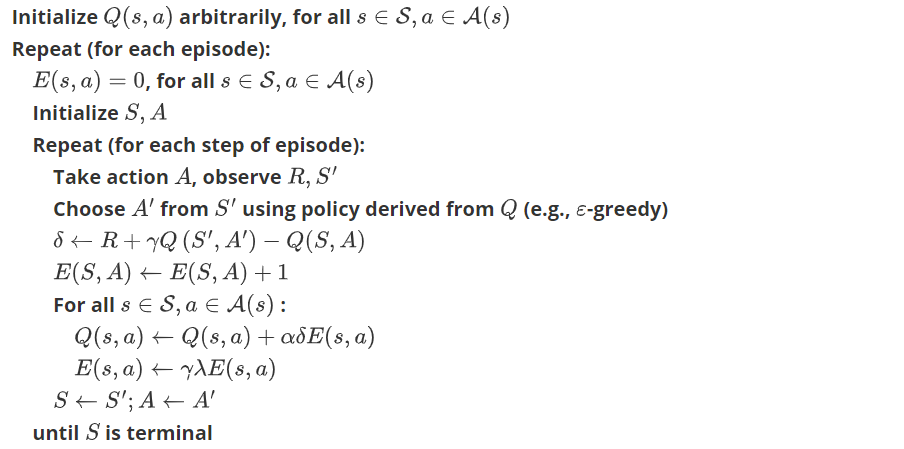
代码实现

class SarsaLambdaTable(RL):
    def __init__(self, actions, learning_rate=0.01, reward_decay=0.9, e_greedy=0.9, trace_decay=0.9):
        super(SarsaLambdaTable, self).__init__(actions, learning_rate, reward_decay, e_greedy)
        self.lambda_ = trace_decay # backward view, eligibility trace.
        self.eligibility_trace = self.q_table.copy()

    def check_state_exist(self, state):
        if state not in self.q_table.index:
            to_be_append = pd.Series([0] * len(self.actions),index=self.q_table.columns,name=state,)
            self.q_table = self.q_table.append(to_be_append) # append new state to q table
            self.eligibility_trace = self.eligibility_trace.append(to_be_append) # also update eligibility trace

    def learn(self, s, a, r, s_, a_):
        self.check_state_exist(s_)
        q_predict = self.q_table.loc[s, a]
        if s_ != 'terminal':
            q_target = r + self.gamma * self.q_table.loc[s_, a_]  # next state is not terminal
        else:
            q_target = r  # next state is terminal
        error = q_target - q_predict

        # 这里开始不同:
        # 对于经历过的 state-action, 我们让他+1, 证明他是得到 reward 路途中不可或缺的一环
        # Method 1:
        # self.eligibility_trace.loc[s, a] += 1

        # Method 2:
        self.eligibility_trace.loc[s, :] *= 0
        self.eligibility_trace.loc[s, a] = 1

        # Q update
        self.q_table += self.lr * error * self.eligibility_trace

        # decay eligibility trace after update
        self.eligibility_trace *= self.gamma*self.lambda_
        

def update():
    for epis in range(100):
        observation = env.reset()
        action = RL.choose_action(str(observation))
        RL.eligibility_trace *= 0 # eligibility trace 只是记录每个回合的每一步, 新回合开始的时候需要将 Trace 清零.
        
        while True:
            ....

Q-Learning

学习目标

训练最优价值函数$Q^\star(s,a)$

TD Target: \[ y_t=r_t+\gamma \cdot \max _a Q^{\star}\left(s_{t+1}, a\right) . \] 利用Q-learning更新DQN

数学推导

通过Sarsa部分推导,对于所有的 $\pi$, \[ Q_\pi\left(s_t, a_t\right)=\mathbb{E}\left[R_t+\gamma \cdot Q_\pi\left(S_{t+1}, A_{t+1}\right)\right] . \] 如果选择最优的策略$\pi^\star$ \[ Q_{\pi^{\star}}\left(s_t, a_t\right)=\mathbb{E}\left[R_t+\gamma \cdot Q_{\pi^{\star}}\left(S_{t+1}, A_{t+1}\right)\right] . \] $Q_{\pi^{\star}}$ 和 $Q^{\star}$ 都表示最优动作价值函数

Identity: $Q^{\star}\left(s_t, a_t\right)=\mathbb{E}\left[R_t+\gamma \cdot Q^{\star}\left(S_{t+1}, A_{t+1}\right)\right]$.

动作$A_{t+1}$通过以下公式计算 \[ A_{t+1}=\underset{a}{\operatorname{argmax}} Q^{\star}\left(S_{t+1}, a\right) . \]

因此 $Q^{\star}\left(S_{t+1}, A_{t+1}\right)=\max _a Q^{\star}\left(S_{t+1}, a\right)$.

所以$Q^{\star}\left(s_t, a_t\right)=\mathbb{E}\left[R_t+\gamma \cdot \max _aQ^{\star}\left(S_{t+1}, a\right)\right]$.

期望直接求比较困难,所以利用蒙特卡洛近似,$R_t$利用观测值$r_t$近似,$S_{t+1}$利用观测值$s_{t+1}$近似得到: \[ Q^{\star}\left(s_t, a_t\right)=\mathbb{E}\left[R_t+\gamma \cdot \max _aQ^{\star}\left(S_{t+1}, a\right)\right]\approx\mathbb{E}\left[r_t+\gamma \cdot \max _aQ^{\star}\left(s_{t+1}, a\right)\right]=TD\ Target\ y_t \]

由此，可以利用表格形式学习$Q_\pi$,针对离散action、state的情况。也可利用神经网络学习$Q_\pi$ 可以用于连续action、state的DQN方法

表格形式

针对离散状态、离散动作情况,当状态和动作数量变多时，表格会越来越大

Observe a transition $\left(s_t, a_t, r_t, s_{t+1}\right)$.
TD target: $y_t=r_t+\gamma \cdot \max _a Q^{\star}\left(s_{t+1}, a\right)$.
TD error: $\delta_t=Q^{\star}\left(s_t, a_t\right)-y_t$.
Update: $\quad Q^{\star}\left(s_t, a_t\right) \leftarrow Q^{\star}\left(s_t, a_t\right)-\alpha \cdot \delta_t$.

算法：

实现代码

class QLearningTable:
    """
    Q-learning算法
    """
    def __init__(self, actions, learning_rate=0.01, reward_decay=0.9, e_greedy=0.9):
        ...
        # 横轴为ations, 纵轴为states
        self.q_table = pd.DataFrame(columns=self.actions, dtype=np.float64)

    def choose_action(self, observation):
        """
        选择 action
        """
        self.check_state_exist(str(observation))
        p_actions = self.q_table.loc[observation, :]

        if np.random.uniform() < self.epsilon:
            return np.random.choice(p_actions[p_actions == np.max(p_actions)].index)
        else:
            return np.random.choice(self.actions)

    def learn(self, s, a, r, s_):
        """
        更新模型参数 动作-状态价值函数（Q值）
        """
        self.check_state_exist(s_)

        # Q(st,at) 原始估计
        q_predict = self.q_table.loc[s, a]

        # 利用reward,state_计算Q_(st,at)新的估计值
        q_target = r + self.gamma * self.q_table.loc[s_, :].max()

        # 利用贝尔曼方程更新Q(st,at)的值
        self.q_table.loc[s, a] += self.lr * (q_target - q_predict)

    def check_state_exist(self, state):
        """
        检查当前的状态是否在q-table表中出现，不存在则添加一行
        """
        if state not in self.q_table.index:
            self.q_table = self.q_table.append(pd.Series([0] * len(self.actions),index=self.q_table.columns,name=state))

# evaluate the reward of q-table
def rollout(RL, env, printout=False):
    ...

def train(q_table, env):
    """
    train the q-table with compilerGym env
    """
    step = 0

    for episode in range(1, FLAGS.episodes + 1):
        # 初始化环境
        observation = env.reset()[FLAGS.features_indices]

        for step_episode in range(FLAGS.episode_length):

            # DQN 根据观测值选择行为
            action = q_table.choose_action(str(observation))
            action_label = FLAGS.flags[action]

            # 环境根据action给出下一个state，reward，是否终止
            observation_, reward, done, info = env.step(env.action_space.flags.index(action_label))
            observation_ = observation_[FLAGS.features_indices]

            # 通过给出反馈，更新模型参数
            q_table.learn(str(observation), action, reward, str(observation_))

            # 将下一个 state_ 变为 下次循环的 state
            observation = observation_

            # 如果终止, 就跳出循环
            if done:
                break

            step += 1

DQN（网络形式）

学习目标：更新网络参数$w$,学习最优动作价值函数$Q^\star$

局限性：动作要求是离散的，当动作维度增大时，神经网络的规模会指数增加

利用神经网络 DQN, $Q(s, a ; \mathbf{w})$ 近似 $Q^{\star}(s, a)$，用神经网络拟合状态到Q值之间的映射关系。状态作为神经网络的输入，可以在连续范围内取值，最终输出得到的是该状态下对应每个动作的Q值，然后我们可以在其中选择一个令Q值最大的作为最优动作。

网络的输入为State，输出为各Action的Q

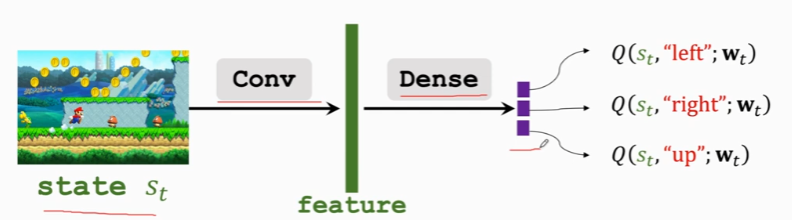
通过DQN网络输出的最大Q值的动作 $a_t=\underset{a}{\operatorname{argmax}} Q\left(s_t, a ; \mathbf{w}\right)$控制agent做动作

Observe a transition $\left(s_t, a_t, r_t, s_{t+1}\right)$.
TD target: $y_t=r_t+\gamma \cdot \max _a Q\left(s_{t+1}, a;w\right)$.
TD error: $\delta_t=Q\left(s_t, a_t;w\right)-y_t$.
Loss: $L_t=\frac{1}{2}[Q(s_t,a_t;w)-y_t]^2$
Update: $w \leftarrow w-\alpha \cdot \delta_t\cdot\frac{\partial Q(s_t,a_t;w)}{\partial w}$.

Multi-Step TD Target

Sarsa vs Q-learning

Sarsa 训练动作价值函数（action-value function）$Q\pi(s,a)$

TD Target: $y_t=r_t+\gamma \cdot Q_\pi\left(s_{t+1}, a_{t+1}\right)$

Q-Learning训练最优动作价值函数（optimal action-value function）$Q^\star (s,a)$

TD Target: $y_t=r_t+\gamma \cdot \max _a Q^{\star}\left(s_{t+1}, a\right)$

前面学习的Sarsa以及Q-Learning都是只使用一个transition$(s_t,a_t,r_t,s_{t+1})$ 其中包含一个reward，称为One-Step TD Target

此外可以同时使用多步transition中的$r_t,r_{t+1},r_{t+2}...r_{t+m-1}$进行更新，这样比单步的学习效果更好。由于包含多步reward，因此Q值更加接近于真实值

数学推导

\[ \begin{aligned} U_{t}&=R_{t}+\gamma \cdot U_{t+1} \\&=R_{t}+\gamma \cdot R_{t+1}+\gamma^{2} \cdot U_{t+2} \\&=R_{t}+\gamma \cdot R_{t+1}+\gamma^{2} \cdot R_{t+2}+\gamma^{3} \cdot U_{t+3} \end{aligned} \]

Identity: $U_{t}=\sum_{i=0}^{m-1} \gamma^{i} \cdot R_{t+i}+\gamma^{m} \cdot U_{t+m} .$

m-step TD target应用于Sarsa算法 \[ y_{t}=\sum_{i=0}^{m-1} \gamma^{i} \cdot r_{t+i}+\gamma^{m} \cdot Q_\pi(s_{t+m},a_{t+m}) . \]

m-step TD target应用于Q-Learing算法 \[ y_{t}=\sum_{i=0}^{m-1} \gamma^{i} \cdot r_{t+i}+\gamma^{m} \cdot \max _aQ^\star(s_{t+m},a) . \]

如果将m设置为1，则为标准的Sarsa、Q-Learning算法

经验回放

在前面DQN+TD-Learning中依次利用各$transition(s_t,a_t,r_t,s_{t+1}),t=1,2,..$来更新网络参数$w$，更新后丢弃此transition不再使用

在实际环境中$s_t$ 与$s_{t+1}$之间有非常明显的相关性，这种相关性对模型的训练是有害的，如果能打散这种相关性，则有利于提升模型的训练效率

因此可以将最近的n条transition保存在一个大小为n队列（memory）中，如果memory满了，则利用最老的memory进行替换

Find $\mathbf{w}$ by minimizing $L(\mathbf{w})=\frac{1}{T} \sum_{t=1}^T \frac{\delta_t^2}{2}$.

Stochastic gradient descent (SGD): (一般使用mini-bach的方法，抽取一组transition，计算loss的平均值来更新网络参数)

Randomly sample a transition, $\left(s_i, a_i, r_i, s_{i+1}\right)$, from the buffer.
Compute TD error, $\delta_i$.
Stochastic gradient: $\mathbf{g}_i=\frac{\partial \delta_i^2 / 2}{\partial \mathbf{w}}=\delta_i \cdot \frac{\partial Q\left(s_i, a_i ; \mathbf{w}\right)}{\partial \mathbf{w}}$
SGD: $\mathbf{w} \leftarrow \mathbf{w}-\alpha \cdot \mathbf{g}_i$.

特点：

可重复利用历史transition，记忆库 (用于重复学习)
打破transition之间的相关性，暂时冻结 q_target 参数 (切断相关性)

算法

# 计算DQN的reward
def rollout(RL, env, printout=False):
    ...

def train(RL, env):
    """
    训练DQN
    """
    # 记录历史reward
    history_reword = []
    step = 0
    for episode in range(1, FLAGS.episodes + 1):
        # 初始化环境
        observation = env.reset()[FLAGS.features_indices]
        for step_episode in range(FLAGS.episode_length):
            action = RL.choose_action(observation) # DQN 根据观测值选择行为
            action_label = FLAGS.flags[action]

            # 环境根据action给出下一个state，reward，是否终止
            observation_, reward, done, info = env.step(env.action_space.flags.index(action_label))
            observation_ = observation_[FLAGS.features_indices]

            # DQN 记录s, a, r, s_,用于获取更新网络参数
            RL.store_transition(observation, action, reward, observation_)

            # 控制学习的起始时间和频率（先累积一些记忆再开始学习）
            if (step > 200) and (step % 5 == 0):
                RL.learn()

            observation = observation_

            # 如果终止, 就跳出循环
            if done:
                break

            step += 1
    
          ...

神经网络与思维决策

搭建两个神经网络（见高估问题 Target Network）

Target Network 用于计算值TD Target, 不会及时更新参数
DQN用于控制agent做运动，并收集transition, 这个神经网络拥有最新的神经网络参数.

# 定义网络结构，三层神经网络
class Net(nn.Module):
    def __init__(self, n_feature, n_hidden, n_output):
        super(Net, self).__init__()
        self.el = nn.Linear(n_feature, n_hidden)
        self.q = nn.Linear(n_hidden, n_output)

    def forward(self, x):
        x = self.el(x)
        x = F.relu(x)  # relu作为激活函数
        x = self.q(x)
        return x


class DeepQNetwork():
    def __init__(self, n_actions, n_features, n_hidden=20, learning_rate=0.01, reward_decay=0.9, e_greedy=0.9,
                 replace_target_iter=200, memory_size=500, batch_size=32, seed=None, e_greedy_increment=None,
                 ):
        self.n_actions = n_actions  # action维度
        self.n_features = n_features  # observation/state维度
        self.n_hidden = n_hidden  # 隐藏层神经元个数
        self.lr = learning_rate  # 学习率
        self.gamma = reward_decay  # 回报衰退率
        self.replace_target_iter = replace_target_iter  # 替换target网络参数的步数
        self.memory_size = memory_size  # 记录的size
        self.memory_counter = 0  # memory当前记录的idx
        self.batch_size = batch_size
        self.epsilon_max = e_greedy
        self.epsilon_increment = e_greedy_increment
        
        # 选择网络预测action的概率，一开始随机选择action，随着训练逐步增大
        self.epsilon = 0 if e_greedy_increment is not None else self.epsilon_max  
        
        self.learn_step_counter = 0  # total learning step
        self.memory = np.zeros((self.memory_size, n_features * 2 + 2))  # initialize zero memory [s, a, r, s_]

        if seed is not None:
            self.set_random_seed(seed)

        self.loss_func = nn.MSELoss()  # 均方误差
        self.cost_his = []  # 记录cost的历史值

        # 构建网络
        self._build_net()

    def _build_net(self):
        """
        初始化网络
        """
        # 创建 eval 神经网络, 及时提升参数
        self.q_eval = Net(self.n_features, self.n_hidden, self.n_actions)

        # 创建 target 神经网络, 提供 target Q
        self.q_target = Net(self.n_features, self.n_hidden, self.n_actions)

        # 使用RMSprop作为优化器
        self.optimizer = torch.optim.RMSprop(self.q_eval.parameters(), lr=self.lr)

    def store_transition(self, s, a, r, s_):
        """
        记录历史的state、action、reward、state_
        """
        # 记录一条 [s, a, r, s_] 记录
        transition = np.hstack((s, [a, r], s_))

        # 总 memory 大小是固定的, 如果超出总大小, 旧 memory 就被新 memory 替换
        index = self.memory_counter % self.memory_size
        self.memory[index, :] = transition
        self.memory_counter += 1

    def choose_action(self, observation):
        """
        利用q_eval网络 根据观测值选择行为
        """
        # 将一维数据转换成矩阵
        # x[:, np.newaxis] ：放在后面，会给列上增加维度；
        # x[np.newaxis, :] ：放在前面，会给行上增加维度；
        observation = torch.Tensor(observation[np.newaxis, :])

        if np.random.uniform() < self.epsilon:
            # 让 eval_net 神经网络生成所有 action 的值, 并选择值最大的 action
            actions_value = self.q_eval(observation)
            action = np.argmax(actions_value.data.numpy())
        else:
            # 随机选择action
            action = np.random.randint(0, self.n_actions)

        return action

    def learn(self):
        """
        更新网络参数
        :return:
        """
        # 更新 target_net 参数
        if self.learn_step_counter % self.replace_target_iter == 0:
            self.q_target.load_state_dict(self.q_eval.state_dict())

        # 从 memory 中随机抽取 batch_size 大小记忆
        if self.memory_counter > self.memory_size:
            sample_index = np.random.choice(self.memory_size, size=self.batch_size)
        else:
            sample_index = np.random.choice(self.memory_counter, size=self.batch_size)
        batch_memory = self.memory[sample_index, :]
        
        # 计算target_net的q值
        q_next = self.q_target(torch.Tensor(batch_memory[:, -self.n_features:])) 
        # 计算eval_net的q值
        q_eval = self.q_eval(torch.Tensor(batch_memory[:, :self.n_features])) 
        
        # =========== 计算loss值 ==============
        # 将q_eval的值复制到q_target
        q_target = torch.Tensor(q_eval.data.numpy().copy())	
        batch_index = np.arange(self.batch_size, dtype=np.int32)
        
        # 每transition的action
        eval_act_index = batch_memory[:, self.n_features].astype(int) 
        
        # 每transition的reward
        reward = torch.Tensor(batch_memory[:, self.n_features + 1])	

        # q_target每个样本对应action的概率赋值为reward + gamma * maxQ(s_)
        # torch.max(q_next, 1)[0] 选择每一行的最大值组成一个列表
        q_target[batch_index, eval_act_index] = reward + self.gamma * torch.max(q_next, 1)[0]
        loss = self.loss_func(q_eval, q_target)	# 将 (q_target - q_eval) 作为误差
        
        """
        
        只需要选择好的 action 的值, 其他的并不需要.
        所以我们将其他的 action 值全变成 0, 将用到的 action 误差值 反向传递回去, 作为更新凭据.
        这是我们最终要达到的样子, 比如 q_target - q_eval = [1, 0, 0] - [-1, 0, 0] = [2, 0, 0]
        q_eval = [-1, 0, 0] 表示这一个记忆中有我选用过 action 0, 而 action 0 带来的 Q(s, a0) = -1, 所以其他的 Q(s, a1) = Q(s, a2) = 0.
        q_target = [1, 0, 0] 表示这个记忆中的 r+gamma*maxQ(s_) = 1, 而且不管在 s_ 上我们取了哪个 action,
        我们都需要对应上 q_eval 中的 action 位置, 所以就将 1 放在了 action 0 的位置

        假如在这个 batch 中, 我们有2个提取的记忆, 根据每个记忆可以生产3个 action 的值:
        q_eval =
        [[1, 2, 3],
         [4, 5, 6]]

        q_target = q_eval =
        [[1, 2, 3],
         [4, 5, 6]]

        然后根据 memory 当中的具体 action 位置来修改 q_target 对应 action 上的值:
        比如在:
            记忆 0 的 q_target 计算值是 -1, 而且我用了 action 0;
            记忆 1 的 q_target 计算值是 -2, 而且我用了 action 2:
        q_target =
        [[-1, 2, 3],
         [4, 5, -2]]

        所以 (q_target - q_eval) 就变成了:
        [[(-1)-(1), 0, 0],
         [0, 0, (-2)-(6)]]

        最后我们将这个 (q_target - q_eval) 当成误差, 反向传递会神经网络.
        所有为 0 的 action 值是当时没有选择的 action, 之前有选择的 action 才有不为0的值.
        我们只反向传递之前选择的 action 的值
        """

        # 反向传递会神经网络
        self.optimizer.zero_grad()
        loss.backward()
        self.optimizer.step()

        # 逐步增大选择网络预测aciton的概率
        self.epsilon = self.epsilon + self.epsilon_increment if self.epsilon < self.epsilon_max else self.epsilon_max
        self.cost_his.append(loss) # 记录历史的cost值
        self.learn_step_counter += 1

优先经验回放

前面的算法在抽样时平等的看待每条transition，但是真实环境中每条transition的重要性是不同的，利用带权重的抽样来代替均匀抽样体现不同transition的重要性

Option 1: Sampling probability $p_t \propto\left|\delta_t\right|+\epsilon$.

Option 2: Sampling probabilit $p_t \propto \frac{1}{\operatorname{rank}(t)}$.

The transitions are sorted so that $\left|\delta_t\right|$ is in the descending order.
$\operatorname{rank}(t)$ is the rank of the $t$-th transition.

TD Error $|\delta_t|$越大表示transition被抽到的概率也就越大

不同的transition有不同的抽样概率，这样会导致DQN的预测有偏差，需要相应的调整学习率，较大的抽样概率应该将learning-rate降低。

Scale the learning rate by $\left(n p_t\right)^{-\beta}$ where $\beta \in(0,1)$

需要记录每条transition的TD Error $\delta_t$，如果一条transition刚收集到并不知道$\delta_t$,则直接设置为最大值（最高的权重） \[ \begin{aligned} &\begin{array}{ccc} \text { Transitions } &\text {Sampling Probabilities } &\text {Learning Rates } \\ \ldots & \ldots & \ldots \\\left(s_t, a_t, r_t, s_{t+1}\right), \delta_t & p_t \propto\left|\delta_t\right|+\epsilon & \alpha \cdot\left(n p_t\right)^{-\beta} \\ \left(s_{t+1}, a_{t+1}, r_{t+1}, s_{t+2}\right), \delta_{t+1} & p_{t+1} \propto\left|\delta_{t+1}\right|+\epsilon & \alpha \cdot\left(n p_{t+1}\right)^{-\beta} \\ \left(s_{t+2}, a_{t+2}, r_{t+2}, s_{t+3}\right), \delta_{t+2} & p_{t+2} \propto\left|\delta_{t+2}\right|+\epsilon & \alpha \cdot\left(n p_{t+2}\right)^{-\beta} \\ \ldots & \ldots & \ldots \end{array} \end{aligned} \] 越高的TD Error $|\delta_t|$ ，更高的概率（权重）被选择，更小的learning-rate

高估问题

TD Learning会导致DQN高估动作价值（action-value），由于以下两个原因

计算TD Target时，$y_t=r_t+\gamma \cdot \max _a Q\left(s_{t+1}, a;w\right) .$用到了最大化操作，导致TD Target大于真实值
Bootstrapping，计算TD Target时，利用了t+1时刻的网络估计

两个原因导致高估问题越来越严重（恶性循环）

非均匀的高估会导致问题，例如某一时刻： \[ \begin{aligned} & Q^{\star}\left(s, a^1\right)=200, Q^{\star}\left(s, a^2\right)=100, and\ Q^{\star}\left(s, a^3\right)=230 \\ & Q\left(s, a^1 ; \mathbf{w}\right)=280, Q\left(s, a^2 ; \mathbf{w}\right)=300, Q\left(s, a^3 ; \mathbf{w}\right)=240 . \end{aligned} \]

Then $a^2$ (which is bad) will be selected.

Target Network

核心思想：利用一个Target Network计算TD

Target network: $Q\left(s, a ; \mathbf{w}^{-}\right)$

与 DQN, $Q(s, a ; \mathbf{w})$ 具有相同的网络结构.
但网络参数不同 $\mathbf{w}^{-} \neq \mathbf{w}$.

利用 $Q(s, a ; \mathbf{w})$ 控制agent做运动，并收集transition: \[ \left\{\left(s_t, a_t, r_t, s_{t+1}\right)\right\} . \]

利用Target Network $Q\left(s, a ; \mathbf{w}^{-}\right)$ 计算TD target: \[ y_t=r_t+\gamma \cdot \max _a Q\left(s_{t+1}, a ; \mathbf{w}^{-}\right) . \]

Target Network参数更新（每隔一段时间）：

Option 1: $\mathbf{w}^{-} \leftarrow \mathbf{w}$.（直接赋值）
Option 2: $\mathbf{w}^{-} \leftarrow \tau \cdot \mathbf{w}+(1-\tau) \cdot \mathbf{w}^{-}$.（做加权平均）

Double DQN

核心思想：利用Double DQN缓解因为maximization导致的高估

原始方法计算TD Target \[ y_t=r_t+\gamma \cdot \max _a Q\left(s_{t+1}, a ; \mathbf{w}\right) . \] 计算TD Target的过程可以分解为两步

选择action: $a^{\star}=\underset{a}{\operatorname{argmax}} Q\left(s_{t+1}, a ; \mathbf{w}\right) .$
计算TD Target: $y_t=r_t+\gamma \cdot Q\left(s_{t+1}, a^{\star} ; \mathbf{w}\right) .$

原始方法中两步均使用DQN，Target Network方法中两步均使用target-net。

Double DQN 第一步使用DQN选择aciton，第二步使用target-net计算TD Target

Selection using DQN: \[ a^{\star}=\underset{a}{\operatorname{argmax}} Q\left(s_{t+1}, a ; \mathbf{w}\right) . \]

Evaluation using target network: \[ y_t=r_t+\gamma \cdot Q\left(s_{t+1}, a^{\star} ; \mathbf{w}^{-}\right) . \] 通过Double DQN的方法大幅提高性能，减少maximization带来的高估问题（但没有彻底根除）

	Selection	Evaluation
Naive Update	DQN	DQN
Using Target	Target Network	Target Network
Double DQN	DQN	Target Network

Dueling Network

Advantage Function

Discounted return: $U_t=R_t+\gamma \cdot R_{t+1}+\gamma^2 \cdot R_{t+2}+\gamma^3 \cdot R_{t+3}+\cdots$

Action-value function: $Q_\pi\left(s_t, a_t\right)=\mathbb{E}\left[U_t \mid S_t=s_t, A_t=a_t\right] \text {. }$

State-value function: $ V_(s_t)=_A$

Optimal action-value function: $Q^{\star}(s, a)=\max _\pi Q_\pi(s, a) \text {. }$

Optimal state-value function: $V^{\star}(s)=\max _\pi V_\pi(s) \text {. }$

Definition: Optimal advantage function.（优势函数） \[ A^{\star}(s, a)=Q^{\star}(s, a)-V^{\star}(s) \text {. } \] $V^{\star}(s)$评价状态s的好坏，$Q^{\star}(s, a)$评价在状态s的情况下做动作a的好坏

$A^{\star}(s, a)$表示动作a相对于baseline的优势，a越好，优势越大

经过数学推导得到以下两个等式

Equation 1: $Q^{\star}(s, a)=V^{\star}(s)+A^{\star}(s, a)$.
Equation 2: $Q^{\star}(s, a)=V^{\star}(s)+A^{\star}(s, a)-\max _a A^{\star}(s, a)$.

$\max _a A^{\star}(s, a)$ 恒等于0，在训练中能保持神经网络的稳定，避免$V^{\star}(s;w),A^{\star}(s, a;w)$两个神经网络的输出随意上下波动

对于Equation 2 \[ Q^{\star}(s, a)=V^{\star}(s)+A^{\star}(s, a)-\max _a A^{\star}(s, a) \]

利用神经网络$V\left(s ; \mathbf{w}^V\right)$近似$V^{\star}(s)$
利用神经网络$A\left(s, a ; \mathbf{w}^A\right)$近似$A^{\star}(s, a)$

因此 $Q^{\star}(s, a)$ 可以利用dueling network表示为： \[ Q(s, a ; \mathbf{w}^A, \mathbf{w}^V)=V(s ; \mathbf{w}^V)+A(s, a ; \mathbf{w}^A)-\max _a A(s, a ; \mathbf{w}^A) .. \]

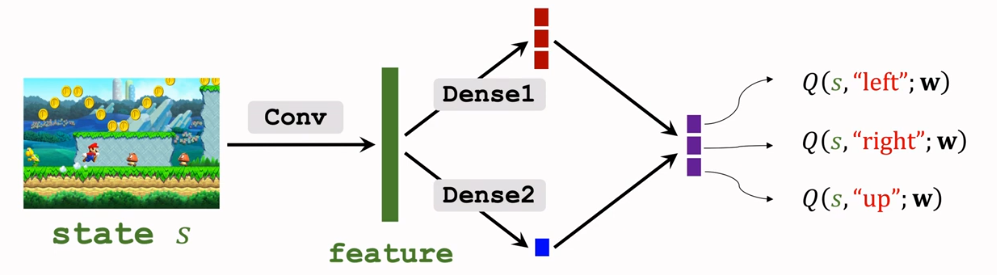
红色对应$A(s, a ; \mathbf{w}^A)$，蓝色对应$V(s ; \mathbf{w}^V)$，将蓝色实数与上面向量每个元素相加，再减去红色向量中的最大元素得到紫色向量（最终输出）

Dueling Network的输入输出、功能、训练方式(TD Learning)、优化方法(Experience Replay, Target Network,double DQN)与DQN完全一样

Dueling Network改变了网络结构，提高了训练效果，此外在实际训练中max可以取mean，有更好的效果 \[ Q(s, a ; \mathbf{w})=V(s ; \mathbf{w}^V)+A(s, a ; \mathbf{w}^A)-\operatorname{mean}_a A(s, a ; \mathbf{w}^A) . \]